强化练习 2020年人教版数学小学四年级上册 8、数学广角—优化——排队问题
海选初战
1.在港口,有4艘轮船都等着卸货,需要的时间分别为4小时、5小时、1小时、10小时。要使4艘轮船所用的等待时间最少,应该按什么样的顺序卸货?最少总等待多少小时?
2.王老师找甲、乙、丙、丁四名学生谈话,甲要8分钟谈完,乙要14分钟谈完,丙要10分钟谈完,丁要5分钟谈完。如何安排四人的谈话顺序可使四人花的总时间最少?最少是多少分钟?
3.有81根火柴,两人轮流拿,规定每个人每次至少要拿走1根,最多拿走3根,直到拿完为止,哪个先拿到最后一根火柴哪个获胜。问取胜的方案是什么。
4.一个探险者筹备穿过长100千米的沙漠,他一天能走20千米,最多可以携带够4天用的食物和水。因此,他需要在途中打造一个中转站补充后几天所需要的食物和水。这个探险者该如何安排他的行程?他需要几天才能穿过这个沙漠?
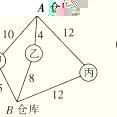
5.A仓库有货物35吨,B仓库有货物25吨,需要运到甲、乙、丙三个工厂去。其中甲工厂需要28吨,乙工厂需要17吨,丙工厂需要15吨。两个仓库与各工厂之间的距离如下图所示(单位:千米),已知运输每吨货物1千米的成本是1元,那样将货物按需要运入各工厂的最少成本是多少元?
开放闯关
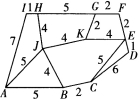
1.某城市交通道路如图所示,数字表示各段路程(单位:千米),求出图中从A到F的最短路程。
2.有1997名少先队员分散在一条公路上值勤宣传交通法规.问完成任务后应该在公路的什么地址集合,可以使他们从各自的宣传职位沿公路走到集合地址的路程总和最小?
实践操练
1.在黑板上写有100个数:
1,2,3,…,100。甲、乙两人轮流擦去黑板上的一个数(甲先擦、乙后擦),假如最后剩下的两个数互质,则乙胜;不然,甲胜。哪个能必胜?必胜的方案是什么?
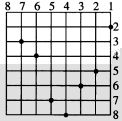
2.C国小镇上的道路设计得好似方格栅栏一样,这种道路设计刚开始在古希腊用。七个好朋友住在镇上七个不一样的地方,用圆点表示,他们想一块聚会喝茶,为使七个人行走的距离和最小,他们应该在城镇的什么地方见面?请用“△”在图中标注出来。
3.一个父亲携带两个儿子去河对岸爬山。河上只有一只空船,船最多能载重80千克,而父亲正好重80千克,两个儿子各重40千克。问他们如何才能全部过河。
4.三个客户到同一个柜台去购物,甲需要4分钟,乙需要6分钟,丙需要2分钟。如何安排他们的购买顺序,使他们所花的总时间最少?最少是多少分钟?
答案
海选初战
1.根据1小时、4小时、5小时、10小时的顺序卸货所用的总时间最少。
1×4+4×3+5×2+10×1=36(小时)
2.根据丁→甲→丙→乙的顺序谈话.他们花的总时间最少。
5×4+8×3+2×10+14×1=78(分钟)
3.先拿走1根,将来他们拿A根.他就拿4-A根,就能保证拿到最后一根。
4.把100千米长的沙漠分成相等的5段,每段20千米。
![]()
探险者要在B点储备4天的食物和水。他从A点到B点,剩下3天的食物和水.留下2天的食物和水,返回A点。第三带上3天的食物和水到B点,这个时候共有4天的储备了,再经过4天就能穿过沙漠,他一共走了1+1+1+4=7(天)。
5.B仓库的25吨货物运往甲工厂:25×5=125(元),A仓库的3吨货物运往甲工厂:3×10=30(元),A仓库的17吨货物运往乙工厂:
17×4=68(元),A仓库的15吨货物运往丙工厂:
15×12=180(元),最少成本125+30+68+180=403(元)。
开放闯关
1.从A到F的最短路线是13千米。 (提示:沿AJKGF线路走。)
2.在从某一端数起第999个职位处集合。
[提示:经过尝试发现,当有奇数(2n+1)个人时,集合地址应选在正中间职位![]() 点。]
点。]
实践操练
1.乙必胜。将这100个数分成50组:,,,,,…,,相邻的两个自然数互质,甲擦掉一个自然数,乙随后擦掉同组的另一个自然数,如此一直维持剩下的都是互质的相邻数,所以乙必胜。
2.七个人到竖向近期的地方是七个人中间地方,在第4竖街区;七个人到横向近期的地方是七个人中间的地方,在第5横街区。故他们应在第4竖街区与第5横街区交会处见面。
3.首次:两个儿子先过河,一个儿子划船回来;第二次:父亲划船过河,另一个儿子划船回来;第三次,两个儿子第三划船过河。
4.根据丙→甲→乙的顺序购买.他们所花的总时间最少。
2×3+4×2+6×1=20(分钟)