![]() __________
__________
专题07 反比率函数问题
__________
【考试知识点1】反比率函数的图象与性质
【例1】(2019·湖北中考考试真题)反比率函数![]() ,下列说法不正确的是()
,下列说法不正确的是()
A.图象经过点 B.图象坐落于2、四象限
C.图象关于直线y=x对称 D.y随x的增大而增大
【答案】D
【分析】通过反比率图象上的点的坐标特点,可对A选项做出判断;通过反比率函数图象和性质、增减性、对称性可对其它选项做出判断,得出答案.
【解析】解:由点![]() 的坐标满足反比率函数
的坐标满足反比率函数![]() ,故A是正确的;
,故A是正确的;
由![]() ,双曲线坐落于2、四象限,故B也是正确的;
,双曲线坐落于2、四象限,故B也是正确的;
由反比率函数的对称性,可知反比率函数![]() 关于
关于![]() 对称是正确的,故C也是正确的,
对称是正确的,故C也是正确的,
由反比率函数的性质,![]() ,在每一个象限内,
,在每一个象限内,![]() 随
随![]() 的增大而增大,不在同一象限,不具备此性质,故D是不正确的,
的增大而增大,不在同一象限,不具备此性质,故D是不正确的,
故选:D.
【点睛】考查反比率函数的性质,当![]() 时,在每一个象限内
时,在每一个象限内![]() 随
随![]() 的增大而增大的性质、反比率函数的图象是轴对称图象,
的增大而增大的性质、反比率函数的图象是轴对称图象,![]() 和
和![]() 是它的对称轴,同时也是中心对称图形;熟练学会反比率函数图象上点的坐标特点和反比率函数图象和性质是解答此题的重点.
是它的对称轴,同时也是中心对称图形;熟练学会反比率函数图象上点的坐标特点和反比率函数图象和性质是解答此题的重点.
【变式1-1】(2019·广东中考考试真题)若点![]() ,
,![]() ,
,![]() 在反比率函数
在反比率函数![]() 的图像上,则
的图像上,则![]() 的大小关系是( )
的大小关系是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【分析】依据点A、B、C分别在反比率函数上,可解得![]() 、
、![]() 、
、![]() 的值,然后通过比较大小即可解答.
的值,然后通过比较大小即可解答.
【解析】解:将A、B、C的横坐标代入反比函数![]() 上,
上,
得:y1=-6,y2=3,y3=2,
所以,![]() ;
;
故选C.
【点睛】本题考查了反比率函数的计算,熟练学会是解题的重点.
【变式1-2】(2019·湖南中考考试真题)如图,一次函数![]() 的图象与反比率函数
的图象与反比率函数![]() (
(![]() 为常数且
为常数且![]() )的图象都经过
)的图象都经过![]() ,结合图象,则不等式
,结合图象,则不等式![]() 的解集是()
的解集是()
A.![]() B.
B.![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
【答案】C
【分析】依据一次函数图象在反比率函数图象上方的![]() 的取值范围便是不等式
的取值范围便是不等式![]() 的解集.
的解集.
【解析】解:由函数图象可知,当一次函数![]() 的图象在反比率函数
的图象在反比率函数![]() (
(![]() 为常数且
为常数且![]() )的图象上方时,
)的图象上方时,![]() 的取值范围是:
的取值范围是:![]() 或
或![]() ,
,
∴不等式![]() 的解集是
的解集是![]() 或
或![]() .
.
故选:C.
【点睛】本题是一次函数图象与反比率函数图象的交点问题:主要考查了由函数图象求不等式的解集.借助数形结合是解题的重点.
【考试知识点2】反比率函数k的几何意义
【例2】(2019·江苏中考考试真题)如图,已知A为反比率函数![]() (
(![]() <0)的图像上一点,过点A作AB⊥
<0)的图像上一点,过点A作AB⊥![]() 轴,垂足为B.若△OAB的面积为2,则k的值为( )
轴,垂足为B.若△OAB的面积为2,则k的值为( )
A.2 B.-2 C.4 D.-4
【答案】D
【分析】设A点坐标为,则有AB=-m,OB=n,继而依据三角形的面积公式与反比率函数图象上点的坐标特点即可求得答案.
【解析】设A点坐标为,则有AB=-m,OB=n,
∵S△ABO=![]() =2,
=2,
∴![]() ,
,
∴mn=-4,
又∵点A在反比率函数![]() 的图象上,
的图象上,
∴n=![]() ,
,
∴k=mn=-4,
故选D.
【点睛】本题考查了反比率函数![]() 图象上点的坐标特点与k的几何意义,熟练学会有关内容是解题的重点.
图象上点的坐标特点与k的几何意义,熟练学会有关内容是解题的重点.
【变式2-1】(2019·辽宁中考考试真题)如图,点A在双曲线y=![]() (x>0)上,过点A作AB⊥x轴于点B,点C在线段AB上且BC:CA=1:2,双曲线y=
(x>0)上,过点A作AB⊥x轴于点B,点C在线段AB上且BC:CA=1:2,双曲线y=![]() (x>0)经过点C,则k=_____.
(x>0)经过点C,则k=_____.
【答案】2
【分析】依据反比率函数系数k的几何意义即可得到结论.
【解析】解:连接OC,
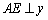
∵点A在双曲线y=![]() (x>0)上,过点A作AB⊥x轴于点B,
(x>0)上,过点A作AB⊥x轴于点B,
∴S△OAB=![]() ×6=3,
×6=3,
∵BC:CA=1:2,
∴S△OBC=3×![]() =1,
=1,
∵双曲线y=![]() (x>0)经过点C,
(x>0)经过点C,
∴S△OBC=![]() |k|=1,
|k|=1,
∴|k|=2,
∵双曲线y=![]() (x>0)在第一象限,
(x>0)在第一象限,
∴k=2,
故答案为2.
【点睛】本题考查了反比率函数的图象与性质,反比率函数图象上点的坐标特点,反比率函数系数k的几何意义,熟练学会反比率函数系数k的几何意义是解题的重点.
【变式2-2】(2019·湖南中考考试真题)如图所示,在直角平面坐标系![]() 中,点
中,点![]() 为反比率函数
为反比率函数![]() 上不一样的三点,连接
上不一样的三点,连接![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 分别作
分别作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,记
,记![]() 、
、![]() 、四边形
、四边形![]() 的面积分别为
的面积分别为![]() 、
、![]() 、
、![]() ,则()
,则()
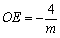
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【分析】依据反比率函数系数![]() 的几何意义得到
的几何意义得到![]() ,即可得到结论.
,即可得到结论.
【解析】解:∵点![]() 为反比率函数
为反比率函数![]() 上不一样的三点,
上不一样的三点, ![]() 轴,
轴, ![]() 垂直
垂直![]() 轴于点
轴于点![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,(故B正确、故A.C错误)
,(故B正确、故A.C错误)
∵![]()
∴![]() ,即D错误.
,即D错误.
故选:B.
【点睛】本题考查了反比率函数系数![]() 的几何意义,反比率函数的性质,正确的辨别图形是解题的重点.
的几何意义,反比率函数的性质,正确的辨别图形是解题的重点.
【变式2-3】(2019·湖南中考考试真题)如图,点A,C分别是正比率函数![]() 的图象与反比率函数
的图象与反比率函数![]() 的图象的交点,过A点作
的图象的交点,过A点作![]() 轴于点D,过C点作
轴于点D,过C点作![]() 轴于点B,则四边形ABCD的面积为___.
轴于点B,则四边形ABCD的面积为___.
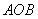
【答案】8
【分析】由反比率函数的对称性可知![]() ,
,![]() ,则
,则![]() ,再依据反比率函数k的几何意义可求得这四个三角形的面积,可求得答案.
,再依据反比率函数k的几何意义可求得这四个三角形的面积,可求得答案.
【解析】![]() A、C是两函数图象的交点,
A、C是两函数图象的交点,
![]() A、C关于原点对称,
A、C关于原点对称,
![]() 轴,
轴,![]() 轴,
轴,
![]() ,
,![]() ,
,
![]() ,
,
又![]() 反比率函数
反比率函数![]() 的图象上,
的图象上,
![]() ,
,
![]() ,
,
故答案为:8.
【点睛】本题主要考查反比率函数的对称性和k的几何意义,依据条件得出![]() ,
,![]() 是解题的重点,注意k的几何意义的应用.
是解题的重点,注意k的几何意义的应用.
【变式2-4】(2019·辽宁中考考试真题)如图,四边形ABCD是矩形,点A在第四象限y1=﹣![]() 的图象上,点B在第一象限y2=
的图象上,点B在第一象限y2=![]() 的图象上,AB交x轴于点E,点C与点D在y轴上,AD=
的图象上,AB交x轴于点E,点C与点D在y轴上,AD=![]() ,S矩形OCBE=
,S矩形OCBE=![]() S矩形ODAE.
S矩形ODAE.
(1)求点B的坐标.
(2)若点P在x轴上,S△BPE=3,求直线BP的分析式.
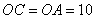
【答案】(1)B(![]() ,2);(2)直线BP的分析式是y=
,2);(2)直线BP的分析式是y=![]() x+1或y=﹣
x+1或y=﹣![]() x+3.
x+3.
【分析】(1)依据反比率函数系数k的几何意义求得k=3,得出![]() ,由题意可知B的横坐标为
,由题意可知B的横坐标为![]() ,代入即可求得B的坐标;
,代入即可求得B的坐标;
(2)设P(a,0),依据三角形面积求得P的坐标,然后依据待定系数法即可求得直线BP的分析式.
【解析】(1)∵S矩形OCBE=![]() S矩形ODAE,点B在第一象限y2=
S矩形ODAE,点B在第一象限y2=![]() 的图象上,
的图象上,
∵点A在第四象限y1=﹣![]() 的图象上,
的图象上,
∴S矩形ODEA=2
∴S矩形OCBE=![]() ×2=3,
×2=3,
∴k=3,
∴y2=![]() ,
,
∵OE=AD=![]() ,
,
∴B的横坐标为![]() ,
,
代入y2=![]() 得,y=
得,y=![]() =2,
=2,
∴B(![]() ,2);
,2);
(2)设P(a,0),
∵S△BPE=![]() PE•BE=
PE•BE=![]() ,
,
解得a=﹣![]() 或
或![]() ,
,
∴点P(﹣![]() ,0)或(
,0)或(![]() ,0),
,0),
设直线BP的分析式为y=mx+n(m≠0),
①若直线过(![]() ,2),(﹣
,2),(﹣![]() ,0),
,0),
则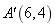 ,解得
,解得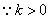 ,
,
∴直线BP的分析式为y=![]() x+1;
x+1;
②若直线过(![]() ,2),(
,2),(![]() ,0),
,0),
则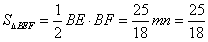 ,解得
,解得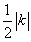 ,
,
∴直线BP的分析式为y=﹣![]() x+3;
x+3;
综上,直线BP的分析式是y=![]() x+1或y=﹣
x+1或y=﹣![]() x+3.
x+3.
【点睛】本题考查了反比率函数系数k的几何意义,反比率函数图象上点的坐标特点,待定系数法求一次函数的分析式,求得B点的坐标是解题的重点.
【考试知识点3】反比率函数的实质应用
【例3】(2019·内蒙古中考考试真题)教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃停止加热,水温开始降低,此时水温![]() (℃)与开机后用时
(℃)与开机后用时![]() (
(![]() )成反比率关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温
)成反比率关系,直至水温降至30℃,饮水机关机,饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时接通电源,水温![]() (℃)与时间
(℃)与时间![]() (
(![]() )的关系如图所示:
)的关系如图所示:
(1)分别写出水温上升和降低阶段![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)怡萱同学想喝高于50℃的水,请问她最多需要等待多久?
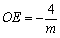
【答案】(1)![]() 与
与![]() 的函数关系式为:
的函数关系式为: 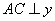 ,
,![]() 与
与![]() 的函数关系式每
的函数关系式每![]() 分钟重复出现一次;(2)她最多需要等待
分钟重复出现一次;(2)她最多需要等待![]() 分钟;
分钟;
【分析】(1)分状况当![]() ,当
,当![]() 时,用待定系数法求解;(2)将
时,用待定系数法求解;(2)将![]() 代入
代入![]() ,得
,得![]() ,将
,将![]() 代入
代入![]() ,得
,得![]() ,可得结果.
,可得结果.
【解析】(1)由题意可得,
![]() ,
,
当![]() 时,设
时,设![]() 关于
关于![]() 的函数关系式为:
的函数关系式为:![]() ,
,
![]() ,得
,得![]() ,
,
即当![]() 时,
时,![]() 关于
关于![]() 的函数关系式为
的函数关系式为![]() ,
,
当![]() 时,设
时,设![]() ,
,
![]() ,得
,得![]() ,
,
即当![]() 时,
时,![]() 关于
关于![]() 的函数关系式为
的函数关系式为![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() 与
与![]() 的函数关系式为:
的函数关系式为: 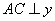 ,
,![]() 与
与![]() 的函数关系式每
的函数关系式每![]() 分钟重复出现一次;
分钟重复出现一次;
(2)将![]() 代入
代入![]() ,得
,得![]() ,
,
将![]() 代入
代入![]() ,得
,得![]() ,
,
∵![]() ,
,![]()
∴怡萱同学想喝高于50℃的水,她最多需要等待![]() 分钟;
分钟;
【点睛】考核要点:一次函数和反比率函数的综合运用.依据实质结合图象剖析问题是重点.
【变式3-1】(2019·湖北中考考试真题)公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来大家把它总结为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬根撬动一块石头,已知阻力和阻力臂分别是![]() 和
和![]() ,则动力
,则动力![]() (单位:
(单位:![]() )关于动力臂l(单位:
)关于动力臂l(单位:![]() )的函数分析式正确的是( )
)的函数分析式正确的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【分析】依据所给公式列式,整理即可得答案.
【解析】∵阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是![]() 和
和![]() ,
,
∴动力![]() 关于动力臂
关于动力臂![]() 的函数分析式为:
的函数分析式为:![]() ,
,
则![]() ,
,
故选B.
【点睛】本题考查了反比率函数的应用,弄清题意,正确剖析各量间的关系是解题的重点.
【变式3-2】(2018·山东中考考试真题)春天是传染病多发的季节,积极预防传染病是学校高度看重的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过![]() 的集中药物喷洒,再封闭宿舍
的集中药物喷洒,再封闭宿舍![]() ,然后打开门窗进行通风,室内每立方米空气中含药量
,然后打开门窗进行通风,室内每立方米空气中含药量![]() 与药物在空气中的持续时间
与药物在空气中的持续时间![]() 之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比率,如图所示.下面四个选项中错误的是( )
之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比率,如图所示.下面四个选项中错误的是( )
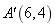
A.经过![]() 集中喷洒药物,室内空气中的含药量最高达到
集中喷洒药物,室内空气中的含药量最高达到![]()
B.室内空气中的含药量高于![]() 的持续时间达到了
的持续时间达到了![]()
C.当室内空气中的含药量高于![]() 且持续时间高于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
且持续时间高于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
D.当室内空气中的含药量低于![]() 时,对人体才是安全的,所以从室内空气中的含药量达到
时,对人体才是安全的,所以从室内空气中的含药量达到![]() 开始,需经过
开始,需经过![]() 后,学生才能进入室内
后,学生才能进入室内
【答案】C
【分析】借助图中信息一一判断即可.
【解析】解: A、正确.不符合题意.
B、由题意x=4时,y=8,∴室内空气中的含药量高于8mg/m3的持续时间达到了11min,正确,不符合题意;
C、y=5时,x=2.5或24,24-2.5=21.5<35,故本选项错误,符合题意;
D、正确.不符合题意,
故选C.
【点睛】本题考查反比率函数的应用、一次函数的应用等常识,解题的重点是了解图象信息,是中考常考试试题型.
【考试知识点4】反比率函数与一次函数综合
【例4】(2019·辽宁中考考试真题)如图,一次函数y=k1x+b的图象与x轴、y轴分别交于A,B两点,与反比率函数y=![]() 的图象分别交于C,D两点,点C(2,4),点B是线段AC的中点.
的图象分别交于C,D两点,点C(2,4),点B是线段AC的中点.
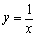
(1)求一次函数y=k1x+b与反比率函数y=![]() 的分析式;
的分析式;
(2)求△COD的面积;
(3)直接写出当x取什么值时,k1x+b<![]() .
.
【答案】(1)y1=x+2;y2=![]() ;(2)S△COD=6;(3)当0<x<2或x<﹣4时,k1x+b<
;(2)S△COD=6;(3)当0<x<2或x<﹣4时,k1x+b<![]() .
.
【分析】(1)把点C的坐标代入反比率函数,借助待定系数法即可求得反比率函数的分析式,作![]() 轴于E,依据题意求得B的坐标,然后借助待定系数法求得一次函数的分析式;
轴于E,依据题意求得B的坐标,然后借助待定系数法求得一次函数的分析式;
(2)联立方程求得D的坐标,然后依据![]() 即可求得△COD的面积;
即可求得△COD的面积;
(3)依据图象即可求得![]() 时,自变量x的取值范围.
时,自变量x的取值范围.
【解析】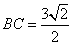
(1)∵点C(2,4)在反比率函数y=![]() 的图象上,
的图象上,
∴![]() ,
,
∴![]() ;
;
如图,作CE⊥x轴于E,
∵C(2,4),点B是线段AC的中点,
∴B(0,2),
∵B、C在![]() 的图象上,
的图象上,
∴![]() ,
,
解得![]() ,
,
∴一次函数为![]() ;
;
(2)由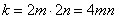 ,
,
解得![]() 或
或![]() ,
,
∴D(﹣4,﹣2),
∴![]() ;
;
(3)由图可得,当0<x<2或x<﹣4时,![]() .
.
【点睛】本题考查了反比率函数和一次函数的交点问题,待定系数法求一次函数和二次函数的分析式,方程组的解与三角形的面积等,求得B点的坐标是解题的重点.
【变式4-1】(2019·广西中考考试真题)已知![]() ,一次函数
,一次函数![]() 与反比率函数
与反比率函数![]() 在同一直角坐标系中的图象可能()
在同一直角坐标系中的图象可能()
A.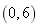 B.
B.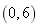
C.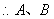 D.
D.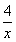
【答案】A
【分析】依据反比率函数图象确定b的符号,结合已知条件求得a的符号,由a,b的符号确定一次函数图象所经过的象限.
【解析】解:若反比率函数![]() 经过1、三象限,则
经过1、三象限,则![]() .所以
.所以![]() .则一次函数
.则一次函数![]() 的图象应该经过1、2、三象限;
的图象应该经过1、2、三象限;
若反比率函数![]() 经过2、四象限,则a<0.所以b>0.则一次函数
经过2、四象限,则a<0.所以b>0.则一次函数![]() 的图象应该经过2、3、四象限.
的图象应该经过2、3、四象限.
故选项A正确;
故选A.
【点睛】本题考查了反比率函数的图象性质和一次函数函数的图象性质,要学会它们的性质才能灵活解题.
【变式4-2】(2019·四川中考考试真题)如图,一次函数![]() 的图象与反比率函数
的图象与反比率函数![]() 的图象交于2、四象限内的点
的图象交于2、四象限内的点![]() 和点
和点![]() .过点
.过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,
,![]() 的面积为4.
的面积为4.
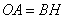
(1)分别求出![]() 和
和![]() 的值;
的值;
(2)结合图象直接写出![]() 的解集;
的解集;
(3)在![]() 轴上取点
轴上取点![]() ,使
,使![]() 获得最大值时,求出点
获得最大值时,求出点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() 或
或![]() ; (3)
; (3)![]()
【分析】(1)依据题意借助三角形面积公式求得![]() ,得到
,得到![]() ,将A代入反比率函数,求出反比率函数分析式,再把B代入分析式,即可解答
,将A代入反比率函数,求出反比率函数分析式,再把B代入分析式,即可解答
(2)依据函数图象结合分析式即可判断
(3)作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,直线
,直线![]() 与
与![]() 轴交于
轴交于![]() ,得到
,得到![]() ,设直线
,设直线![]() 的关系式为
的关系式为![]() ,把将
,把将 ![]() ,
,![]() 代入得到分析式,即可解答
代入得到分析式,即可解答
【解析】(1)∵点![]() ,
,
∴![]() ,
,
∵![]() ,即
,即![]() ,
,
∴![]() ,
,
∵点![]() 在第二象限,
在第二象限,
∴![]()
![]() ,
,
将![]() 代入
代入![]() 得:
得:![]() ,
,
∴反比率函数的关系式为:![]() ,
,
把![]() 代入得:
代入得:![]() ,
,
∴![]()
因此![]() ,
,![]() ;
;
(2)由图象可以看出![]() 的解集为:
的解集为:![]() 或
或![]() ;
;
(3)如图,作点![]() 关于
关于![]() 轴的对称点
轴的对称点![]() ,直线
,直线![]() 与
与![]() 轴交于
轴交于![]() ,
,
此时![]() 最大,
最大,
∵![]()
∴![]()
设直线![]() 的关系式为
的关系式为![]() ,将
,将 ![]() ,
,![]() 代入得:
代入得:![]()
解得:![]() ,
,![]() ,
,
∴直线![]() 的关系式为
的关系式为![]() ,
,
当![]() 时,即
时,即![]() ,解得
,解得![]() ,
,
∴![]()
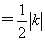
【点睛】此题考查一次函数与反比率函数,解题重点在于把已知点代入分析式
【考试知识点5】反比率函数与几何综合
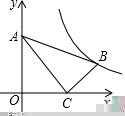
【例5】(2019·山东中考考试真题)已知一次函数![]() 的图象与反比率函数
的图象与反比率函数![]() 的图象交于点
的图象交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,若
,若![]() ,且
,且![]() .
.
(1)求反比率函数与一次函数的表达式;
(2)若点![]() 为x轴上一点,
为x轴上一点,![]() 是等腰三角形,求点
是等腰三角形,求点![]() 的坐标.
的坐标.
【答案】(l)![]() ,
,![]() ;(2)
;(2)![]() 、
、![]() ,
,![]() ,
,![]()
【分析】(1)依据![]() 可计算出A点的纵坐标,进而借助勾股定理计算出A点的横坐标,代入可得一次函数和反比率函数的分析式.
可计算出A点的纵坐标,进而借助勾股定理计算出A点的横坐标,代入可得一次函数和反比率函数的分析式.
(2)依据题意可得有三种状况,一种是AB为底,一种是AB为腰,以A为顶点,一种是AB为腰,以B为顶点.
【解析】(l)过点![]() 作
作![]() 轴于点
轴于点![]()
∵![]()
∴![]()
∴![]()
∵![]() ∴
∴![]()
在![]() 中,
中,![]()
∴![]() ∴
∴![]()
∵![]() 经过点
经过点![]() ∴
∴![]() ∴
∴![]()
∴反比率函数表达式为![]()
∵![]() 经过点
经过点![]() ,点
,点![]()
∴![]() 解得
解得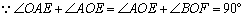
∴一次函数表达式为![]()
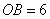
(2)本题分三种状况
①当以![]() 为腰,且点
为腰,且点![]() 为顶角顶点时,可得点
为顶角顶点时,可得点![]() 的坐标为
的坐标为![]() 、
、![]()
②当以![]() 为腰,且以点
为腰,且以点![]() 为顶角顶点时,点
为顶角顶点时,点![]() 关于
关于![]() 的对称点即为所求的点
的对称点即为所求的点![]()
③当以![]() 为底时,作线段
为底时,作线段![]() 的中垂线交
的中垂线交![]() 轴于点
轴于点![]() ,交
,交![]() 于点
于点![]() ,则点
,则点![]() 即为所求
即为所求
由(1)得,![]()
在![]() 中,
中,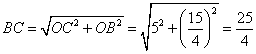
∵![]()
∴![]() ∴
∴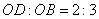 ∴
∴![]() ∴
∴![]()
∴![]()
【点睛】本题主要考查一次函数和反比率函数的综合性问题,重点在于第二问中的等腰三角形,要分AB为腰和底,为腰又要分顶点是A还是B.
【变式5-1】(2019·辽宁中考考试真题)如图,在平面直角坐标系![]() 中,点
中,点![]() 在反比率函数
在反比率函数![]() 的图象上,点
的图象上,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 轴,垂足为
轴,垂足为![]() ,
,![]() 与反比率函数的图象相交于点
与反比率函数的图象相交于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求该反比率函数的分析式;
(2)若![]() ,设点
,设点![]() 的坐标为
的坐标为![]() ,求线段
,求线段![]() 的长.
的长.
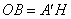
【答案】(1)![]() ;(2)3
;(2)3
【分析】(1)把点A(3,2)代入反比率函数y=![]() ,即可求出函数分析式;
,即可求出函数分析式;
(2)直线OA的关系式可求,因为点C(a,0),可以表示点B、D的坐标,依据
S△ACD=![]() ,打造方程可以解出a的值,进而求出BD的长.
,打造方程可以解出a的值,进而求出BD的长.
【解析】解:
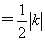
(1)∵点![]() 在反比率函数
在反比率函数![]() 的图象上,
的图象上,
∴![]() ,
,
∴反比率函数![]() ;
;
答:反比率函数的关系式为:![]() ;
;
(2)过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() ,
,
设直线![]() 的关系式为
的关系式为![]() ,将
,将![]() 代入得,
代入得,![]() ,
,
∴直线![]() 的关系式为
的关系式为![]() ,
,
∵点![]() ,把
,把![]() 代入
代入![]() ,得:
,得:![]() ,把
,把![]() 代入
代入![]() ,得:
,得:![]() ,
,
∴![]() ),即
),即![]() ,
,
![]() ,即
,即![]()
∵![]() ,
,
∴![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
∴![]() ;
;
答:线段![]() 的长为3.
的长为3.
【点睛】考查正比率函数的图象和性质、反比率函数的图象和性质,将点的坐标转化为线段的长,借助方程求出所设的参数,进而求出结果是解决此类问题常见的办法.
【变式5-2】(2019·江苏中考考试真题)如图,在平面直角坐标系![]() 中,菱形
中,菱形![]() 的顶点
的顶点![]() 与原点
与原点![]() 重合,顶点
重合,顶点![]() 落在
落在![]() 轴的正半轴上,对角线
轴的正半轴上,对角线![]() 、
、![]() 交于点
交于点![]() ,点
,点![]() 、
、![]() 恰好都在反比率函数
恰好都在反比率函数![]() 的图象上,则
的图象上,则![]() 的值为()
的值为()
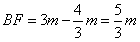
A.![]() B.
B.![]() C.2 D.
C.2 D.![]()
【答案】A
【分析】借助菱形的性质, 依据正切概念即可得到答案.
【解析】解:设![]() ,
,![]() ,
,
∵![]() 点为菱形对角线的交点,
点为菱形对角线的交点,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
把![]() 代入
代入![]() 得
得![]() ,
,
∴![]() ,
,
∵四边形![]() 为菱形,
为菱形,
∴![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() .
.
故选A.
【点睛】本题考查了反比率函数图象上点的坐标特点,解题重点在于运用菱形的性质.
__________
1.(2019·山东中考考试真题)如图,直线l与x轴,y轴分别交于A,B两点,且与反比率函数y=![]() (x>0)的图象交于点C,若S△AOB=S△BOC=1,则k=()
(x>0)的图象交于点C,若S△AOB=S△BOC=1,则k=()
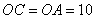
A.1 B.2 C.3 D.4
【答案】D
【分析】作CD⊥x轴于D,设OB=a(a>0).由S△AOB=S△BOC,依据三角形的面积公式得出AB=BC.依据相似三角形性质即可表示出点C的坐标,把点C坐标代入反比率函数即可求得k.
【解析】如图,作CD⊥x轴于D,设OB=a(a>0).
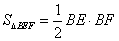
∵S△AOB=S△BOC,
∴AB=BC.
∵△AOB的面积为1,
∴![]() OA•OB=1,
OA•OB=1,
∴OA=![]() ,
,
∵CD∥OB,AB=BC,
∴OD=OA=![]() ,CD=2OB=2a,
,CD=2OB=2a,
∴C(![]() ,2a),
,2a),
∵反比率函数y=![]() (x>0)的图象经过点C,
(x>0)的图象经过点C,
∴k=![]() ×2a=4.
×2a=4.
故选D.
【点睛】此题考查反比率函数与一次函数的交点问题,待定系数法求函数分析式,会运用相似求线段长度是解题的重点.
2.(2019·辽宁中考考试真题)如图,点A在反比率函数y=![]() 的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为
的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为
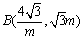
A.3 B.2 C.![]() D.1
D.1
【答案】C
【分析】连结OA,如图,借助三角形面积公式得到S△OAB=S△CAB,再依据反比率函数的比率系数k的几何意义得到S△OAB=![]() |k|,便可求得结果.
|k|,便可求得结果.
【解析】解:连结OA,如图,
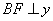
∵AB⊥x轴,
∴OC∥AB,
∴S△OAB=S△CAB,
而S△OAB=![]() |k|=
|k|=![]() ,
,
∴S△CAB=![]() ,
,
故选:C.
【点睛】本题考查了反比率函数的比率系数k的几何意义:在反比率函数y=![]() 图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.
3.(2019·四川中考考试真题)如图,一次函数![]() 和反比率函数
和反比率函数![]() 的图象相交于
的图象相交于![]() ,
,![]() 两点,则使
两点,则使![]() 成立的
成立的![]() 取值范围是
取值范围是
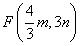
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C.![]() 或
或![]() D.
D.![]() 或
或![]()
【答案】B
【分析】依据图象找出一次函数图象在反比率函数图象上方时对应的自变量的取值范围即可.
【解析】察看函数图象可发现:![]() 或
或![]() 时,一次函数图象在反比率函数图象上方,
时,一次函数图象在反比率函数图象上方,
∴使![]() 成立的
成立的![]() 取值范围是
取值范围是![]() 或
或![]() ,
,
故选B.
【点睛】本题考查了反比率函数与一次函数综合,函数与不等式,借助数形结合思想是解题的重点.
4.(2019·山东中考考试真题)函数![]() 与
与![]() (
(![]() )在同一坐标系中的图象可能是()
)在同一坐标系中的图象可能是()
A.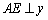 B.
B. C.
C.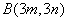 D.
D.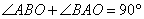
【答案】D
【分析】依据反比率函数与一次函数的图象特征解答即可.
【解析】![]() 时,
时,![]() ,
,![]() 在1、2、四象限,
在1、2、四象限,![]() 在1、三象限,无选项符合.
在1、三象限,无选项符合.
![]() 时,
时,![]() ,
,![]() 在1、3、四象限,
在1、3、四象限,![]() (
(![]() )在2、四象限,只有D符合;
)在2、四象限,只有D符合;
故选:D.
【点睛】本题主要考查了反比率函数的图象性质和一次函数的图象性质,重点是由![]() 的取值确定函数所在的象限.
的取值确定函数所在的象限.
5.(2019·湖北中考考试真题)如图,在平面直角坐标系中,点![]() 在第一象限,
在第一象限,![]() 轴于点
轴于点![]() ,反比率函数
,反比率函数![]() (
(![]() )的图象与线段
)的图象与线段![]() 相交于点
相交于点![]() ,且
,且![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 的坐标为
的坐标为![]() ,若
,若![]() 的面积为3,则
的面积为3,则![]() 的值为( )
的值为( )
A.![]() B.1 C.2 D.3
B.1 C.2 D.3
【答案】D
【分析】依据对称性求出C点坐标,进而得OA与AB的长度,再依据已知三角形的面积列出n的方程求得n,进而用待定系数法求得k.
【解析】∵点C关于直线y=x的对称点C'的坐标为(1,n)(n≠1),
∴C(n,1),
∴OA=n,AC=1,
∴AB=2AC=2,
∵△OAB的面积为3,
∴![]() n×2=3,
n×2=3,
解得,n=3,
∴C(3,1),
∴k=3×1=3.
故选:D.
【点睛】本题是反比率函数图象与一次函数图象的交点问题,主要考查了一次函数与反比率函数的性质,对称性质,重点是依据对称求得C点坐标及由三角形的面积列出方程.
6.(2019·贵州中考考试真题)如图,在平面直角坐标系中,菱形ABCD在第一象限内,边BC与x轴平行,A,B两点的纵坐标分别为4,2,反比率函数y![]() (x>0)的图象经过A,B两点,若菱形ABCD的面积为2
(x>0)的图象经过A,B两点,若菱形ABCD的面积为2![]() ,则k的值为()
,则k的值为()
A.2 B.3 C.4 D.6
【答案】C
【分析】过点A作x轴的垂线,交CB的延长线于点E,依据A,B两点的纵坐标分别为4,2,可得出横坐标,即可求得AE,BE的长,依据菱形的面积为2![]() ,求得AE的长,在Rt△AEB中,即可得出k的值.
,求得AE的长,在Rt△AEB中,即可得出k的值.
【解析】过点A作x轴的垂线,交CB的延长线于点E,
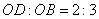
∵A,B两点在反比率函数y![]() (x>0)的图象,且纵坐标分别为4,2,
(x>0)的图象,且纵坐标分别为4,2,
∴A(![]() ,4),B(
,4),B(![]() ,2),
,2),
∴AE=2,BE![]() k
k![]() k
k![]() k,
k,
∵菱形ABCD的面积为2![]() ,
,
∴BC×AE=2![]() ,即BC
,即BC![]() ,
,
∴AB=BC![]() ,
,
在Rt△AEB中,BE![]() 1
1
∴![]() k=1,
k=1,
∴k=4.
故选:C.
【点睛】本题考查了菱形的性质与反比率函数图象上点的坐标特点,熟记菱形的面积公式是解题的重点.
7.(2019·湖北中考考试真题)如图,平面直角坐标系中,![]() ,反比率函数
,反比率函数![]() 的图象分别与线段
的图象分别与线段![]() 交于点
交于点![]() ,连接
,连接![]() .若点
.若点![]() 关于
关于![]() 的对称点恰好在
的对称点恰好在![]() 上,则
上,则![]() ()
()
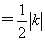
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【分析】依据![]() ,可得矩形的长和宽,易知点
,可得矩形的长和宽,易知点![]() 的横坐标,
的横坐标,![]() 的纵坐标,由反比率函数的关系式,可用含有
的纵坐标,由反比率函数的关系式,可用含有![]() 的代数式表示另外一个坐标,由三角形相似和对称,可用求出
的代数式表示另外一个坐标,由三角形相似和对称,可用求出![]() 的长,然后把问题转化到三角形
的长,然后把问题转化到三角形![]() 中,由勾股定理打造方程求出
中,由勾股定理打造方程求出![]() 的值.
的值.
【解析】过点![]() 作
作![]() ,垂足为
,垂足为![]() ,设点
,设点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,连接
,连接![]() ,如图所示:
,如图所示:
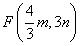
则![]() ,
,
![]()
![]()
易证![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 在反比率函数
在反比率函数![]() 的图象上,
的图象上,
![]()
![]()
![]()
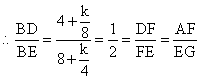
![]() ,
,
在![]() 中,由勾股定理:
中,由勾股定理: ![]()
即:![]()
解得:![]()
故选C.
【点睛】此题综合借助轴对称的性质,相似三角形的性质,勾股定理与反比率函数的图象和性质等常识,发现![]() 与
与![]() 的比是
的比是![]() 是解题的重点.
是解题的重点.
8.(2019·吉林中考考试真题)如图,在平面直角坐标系中,![]() 的顶点
的顶点![]() 、
、![]() 的坐标分别是
的坐标分别是![]() ,
,![]() ,
,![]() ,则函数
,则函数![]() 的图象经过点
的图象经过点![]() ,则
,则![]() 的值为()
的值为()

A.![]() B.9 C.
B.9 C.![]() D.
D.![]()
【答案】D
【分析】依据![]() 、
、![]() 的坐标分别是
的坐标分别是![]() 可知
可知![]() ,进而可求出
,进而可求出![]() ,由
,由![]() ,又可求
,又可求![]() ,通过作垂线架构等腰直角三角形,求出点
,通过作垂线架构等腰直角三角形,求出点![]() 的坐标,再求出
的坐标,再求出![]() 的值.
的值.
【解析】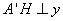
解:过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,
,
∵![]() 的坐标分别是
的坐标分别是![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]()
∴![]() 代入
代入![]() 得:
得:![]() ,
,
故选:D.
【点睛】考核要点:反比率函数与几何.数形结合剖析是重点.
9.(2019·湖南中考考试真题)如图,⊙O的半径为2,双曲线的分析式分别为![]() 和
和![]() ,则阴影部分的面积是
,则阴影部分的面积是
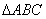
A.4π B.3π C.2π D.π
【答案】C
【分析】依据反比率函数的对称性得出图中阴影部分的面积为半圆面积,进而求出即可.
【解析】双曲线![]() 和
和![]() 的图象关于x轴对称,
的图象关于x轴对称,
依据图形的对称性,把第二象限和第四象限的阴影部分的面积拼到第一和第三象限中的阴影中,可以得到阴影部分就是一个扇形,
并且扇形的圆心角为![]() ,半径为2,
,半径为2,
所以:![]() .
.
故选C.
【点睛】本题考查的是反比率函数,题目中的两条双曲线关于x轴对称,圆也是一个对称图形,可以得到图中阴影部分的面积等于圆心角为180°,半径为2的扇形的面积,用扇形面积公式计算可以求出阴影部分的面积.
10.(2019·重庆中考考试真题)如图,在平面直角坐标系中,菱形OABC的边OA在x轴上,点![]() ,
,![]() .若反比率函数
.若反比率函数![]() 经过点C,则k的值等于( )
经过点C,则k的值等于( )
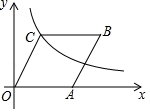
A.10 B.24 C.48 D.50
【答案】C
【分析】由菱形的性质和锐角三角函数可求点![]() ,将点C坐标代入分析式可求k的值.
,将点C坐标代入分析式可求k的值.
【解析】解:如图,过点C作![]() 于点E,
于点E,
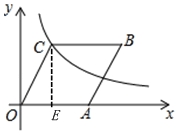
∵菱形OABC的边OA在x轴上,点![]() ,
,
∴![]() ,
,
∵![]() .
.
∴![]() ,
,
∴![]()
∴点C坐标![]()
∵若反比率函数![]() 经过点C,
经过点C,
∴![]()
故选:C.
【点睛】本题考查了反比率函数性质,反比率函数图象上点的坐标特点,菱形的性质,锐角三角函数,重点是求出点C坐标.
11.(2019·湖北中考考试真题)在平面直角坐标系中,将一块直角三角板如图放置,直角顶点与原点![]() 重合,顶点
重合,顶点![]() 恰好分别落在函数
恰好分别落在函数![]() 的图象上,则
的图象上,则![]() 的值为( )
的值为( )
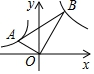
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【分析】点![]() 落在函数
落在函数![]() ,
,![]() 的图象上,依据反比率函数的几何意义,可得直角三角形的面积;依据题意又可知这两个直角三角形相似,而相似比恰好是直角三角形
的图象上,依据反比率函数的几何意义,可得直角三角形的面积;依据题意又可知这两个直角三角形相似,而相似比恰好是直角三角形![]() 的两条直角边的比,再借助勾股定理,可得直角边与斜边的比,从而得出答案.
的两条直角边的比,再借助勾股定理,可得直角边与斜边的比,从而得出答案.
【解析】过点![]() 分别作
分别作![]() 轴,
轴,![]() 轴,垂足为
轴,垂足为![]() ,
,
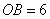
![]() 点
点![]() 在反比率函数
在反比率函数![]() 上,点
上,点![]() 在
在![]() 上,
上,
![]()
又![]()
![]()
![]()
 ,
,
![]()
设![]() 则
则![]()
![]()
在![]()
![]()
故选![]()
【点睛】考查反比率函数的几何意义、相似三角形的性质,将面积比转化为相似比,借助勾股定理可得直角边与斜边的比,求出sin∠ABO的值.
12.(2019·山东中考考试真题)如图,平行四边形AOBC中,对角线交于点E,双曲线y=![]() (k>0)经过A、E两点,若平行四边形AOBC的面积为24,则k的值是()
(k>0)经过A、E两点,若平行四边形AOBC的面积为24,则k的值是()
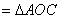
A.8 B.7.5 C.6 D.9
【答案】A
【分析】设出点A的横坐标为x,依据点A在双曲线y=![]() (k>0)上,表示出点A的纵坐标,从而表示出点A的坐标,再依据点B在x轴上设出点B的坐标为(a,0),然后过A作AD⊥OB于D,EF⊥OB于F,如图,依据平行四边形的性质对角线互相平分得到点E为AB的中点,又EF∥AD,得到EF为△ABD的中位线,可得EF为AD的一半,而AD为A的纵坐标,可得出EF的长,由OB-OD可得BD的长,依据F为BD的中点,得到FB的长,由OB-FB可得出OF的长,由E在第一象限,由EF和OF的长表示出E的坐标,代入反比率分析式中,得到a=3x,再由BO与AD的积为平行四边形的面积,表示出平行四边形的面积,依据平行四边形AOBC的面积为24,列出等式,将a=3x代入可得出k的值.
(k>0)上,表示出点A的纵坐标,从而表示出点A的坐标,再依据点B在x轴上设出点B的坐标为(a,0),然后过A作AD⊥OB于D,EF⊥OB于F,如图,依据平行四边形的性质对角线互相平分得到点E为AB的中点,又EF∥AD,得到EF为△ABD的中位线,可得EF为AD的一半,而AD为A的纵坐标,可得出EF的长,由OB-OD可得BD的长,依据F为BD的中点,得到FB的长,由OB-FB可得出OF的长,由E在第一象限,由EF和OF的长表示出E的坐标,代入反比率分析式中,得到a=3x,再由BO与AD的积为平行四边形的面积,表示出平行四边形的面积,依据平行四边形AOBC的面积为24,列出等式,将a=3x代入可得出k的值.
【解析】设A(x,![]() ),B(a,0),过A作AD⊥OB于D,EF⊥OB于F,如图,
),B(a,0),过A作AD⊥OB于D,EF⊥OB于F,如图,
由平行四边形的性质可知AE=EB,
再EF为△ABD的中位线,
由三角形的中位线定理得:![]()
则E ![]()
∵E在双曲线上,
∴![]()
∴a=3x,
∵平行四边形的面积是24,
∴![]()
解得:k=8.
故选:A
【点睛】本题考查的是反比率函数综合题,涉及的常识有:平行线的性质,三角形中位线定理,平行四边形的性质,平行四边形及三角形的面积公式,与点坐标与线段的关系,是一道综合性较强的题,本题的突破点是作出如图的辅助线,打造点坐标与线段长度的联系.
13.(2019·山东中考考试真题)如图,点A的坐标是,点B的坐标是,C为OB的中点,将△ABC绕点B逆时针旋转90°后得到![]() .若反比率函数
.若反比率函数![]() 的图象恰好经过
的图象恰好经过![]() 的中点D,则k的值是()
的中点D,则k的值是()
A.9 B.12 C.15 D.18
【答案】C
【分析】作![]() 轴于
轴于![]() 证明
证明![]() ≌
≌![]() ,推出
,推出![]() ,
,![]() ,求出点
,求出点![]() 坐标,再借助中点坐标公式求出点D坐标即可解决问题.
坐标,再借助中点坐标公式求出点D坐标即可解决问题.
【解析】解:作![]() 轴于
轴于![]() .
.
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵点![]() 的坐标是
的坐标是![]() ,点
,点![]() 的坐标是
的坐标是![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵反比率函数![]() 的图象经过点
的图象经过点![]() ,
,
∴![]() .
.
故选:C.
【点睛】本题考查反比率函数图形上的点的坐标特点,坐标与图形的变化![]() 旋转等常识,解题的重点是掌握添加常用辅助线,架构全等三角形解决问题,是中考选择题中的压轴题.
旋转等常识,解题的重点是掌握添加常用辅助线,架构全等三角形解决问题,是中考选择题中的压轴题.
14.(2019·辽宁中考考试真题)如图,将一个含30°角的三角尺ABC放在直角坐标系中,使直角顶点C与原点O重合,顶点A,B分别在反比率函数y=﹣![]() 和y=
和y=![]() 的图象上,则k的值为___.
的图象上,则k的值为___.
【答案】12.
【分析】过A作AE⊥y轴于E过B作BF⊥y轴于F,通过△AOE∽△BOF,得到![]() ,设
,设![]() ,于是得到AE=-m,
,于是得到AE=-m,![]() ,从而得到
,从而得到![]() ,,于是求得结果.
,,于是求得结果.
【解析】解:过![]() 作
作![]() 轴于
轴于![]() 过
过![]() 作
作![]() 轴于
轴于![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() ,
,
设![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() .
.
故答案为:12.

【点睛】此题考查相似三角形的断定与性质,反比率函数图象上点的坐标特点,解题重点在于作辅助线和借助三角函数进行解答.
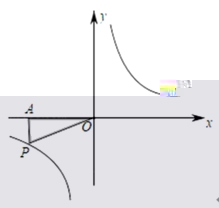
15.(2019·青海中考考试真题)如图,![]() 是反比率函数
是反比率函数![]() 图象上的一点,过点
图象上的一点,过点![]() 向
向![]() 轴作垂线交于点
轴作垂线交于点![]() ,连接
,连接![]() .若图中阴影部分的面积是
.若图中阴影部分的面积是![]() ,则此反比率函数的分析式为_____.
,则此反比率函数的分析式为_____.
【答案】![]() .
.
【分析】依据反比率函数系数![]() 的几何意义可知,
的几何意义可知,![]() 的面积
的面积![]() ,再依据图象所在象限求出
,再依据图象所在象限求出![]() 的值即可.
的值即可.
【解析】解:依据比率系数![]() 的几何意义可得,
的几何意义可得,
![]() 面积等于
面积等于![]() ,
,
即![]() ,
,
![]() ,
,
因为函数图象坐落于1、三象限,则![]() ,
,
![]() 反比率函数的分析式为
反比率函数的分析式为![]() ;
;
故答案为![]() .
.
【点睛】本题考查反比率系数![]() 的几何意义,过双曲线上的任意一点分别向两条坐标作垂线,与坐标轴围成的矩形面积就等于
的几何意义,过双曲线上的任意一点分别向两条坐标作垂线,与坐标轴围成的矩形面积就等于![]() .
.
16.(2019·湖北中考考试真题)如图,一直线经过原点![]() ,且与反比率函数
,且与反比率函数![]()
![]() 相交于点
相交于点![]() 、点
、点![]() ,过点
,过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,连接
,连接![]() .若
.若![]() 面积为
面积为![]() ,则
,则![]() _____.
_____.
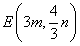
【答案】8
【分析】第一依据反比率函数与正比率函数的图象特点,可知A、B两点关于原点对称,则O为线段AB的中点,故△BOC的面积等于△AOC的面积,都等于4,然后由反比率函数![]() 的比率系数k的几何意义,可知△AOC的面积等于
的比率系数k的几何意义,可知△AOC的面积等于![]() ,从而求出k的值.
,从而求出k的值.
【解析】解:![]() 反比率函数与正比率函数的图象相交于
反比率函数与正比率函数的图象相交于![]() 、
、![]() 两点,
两点,
![]() 两点关于原点对称,
两点关于原点对称,
![]() ,
,
![]() 的面积
的面积![]() 的面积
的面积![]() ,
,
又![]() 是反比率函数
是反比率函数![]() 图象上的点,且
图象上的点,且![]() 轴于点
轴于点![]() ,
,
![]() 的面积
的面积![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
故答案为![]() .
.
【点睛】本题考查反比率函数与一次函数的交点问题,反比率函数的比率系数k的几何意义,解题重点在于得出O为线段AB的中点.
17.(2019·湖北中考考试真题)如图,双曲线![]() 经过矩形OABC的顶点
经过矩形OABC的顶点![]() ,双曲线
,双曲线![]() 交
交![]() ,
,![]() 于点
于点![]() ,
,![]() ,且与矩形的对角线
,且与矩形的对角线![]() 交于点
交于点![]() ,连接
,连接![]() .若
.若![]() ,则
,则![]() 的面积为__________.
的面积为__________.
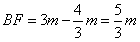
【答案】![]() .
.
【分析】设![]() ,依据题意
,依据题意![]() ,
,![]() ,
,![]() ,即可得出
,即可得出![]() ,
,![]() ,解得
,解得![]() ,由
,由![]() ,
,![]() ,求得
,求得![]() 、
、![]() ,然后依据三角形面积公式得到
,然后依据三角形面积公式得到![]() 进行求解即可.
进行求解即可.
【解析】设![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵双曲线![]() 经过矩形
经过矩形![]() 的顶点
的顶点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵双曲线![]() 经过点
经过点![]() ,
,
∴![]()
∴双曲线![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
故答案为:![]() .
.
【点睛】本题考查了反比率系数 的几何意义和反比率函数图象上点的坐标特点、三角形面积等,表示出每个点的坐标是解题的重点.







